| Заходите к нам на форум: задавайте вопросы - получайте ответы! |
|
Исследование Солнечной Системы - Наблюдения
| |||||
Астрономические наблюдения |
|
Наблюдение двойных звезд
ЧАСТЬ I - ЧАСТЬ II
Тема наблюдения двойных и кратных звезд как-то всегда мягко обходилась стороной в отечественных любительских публикациях, и даже в ранее издававшихся книгах о наблюдении двойных звезд любительскими средствами вы вряд ли найдете обилие информации. Причин этому несколько. Конечно, уже не секрет, что любительские наблюдения двойных мало чего стоят с научной точки зрения, и что профессионалы открыли большую часть таких звезд, а те, которые еще не успели открыть или изучить, настолько недоступны рядовым любителям, как и полет последних на Марс. Точность любительских измерений значительно ниже, чем у астрономов, работающих на больших и точных инструментах, определяющих характеристики звездных пар иногда даже выходящих за пределы видимости, используя лишь математический аппарат для описания таких систем. Все эти причины не могут оправдать столь поверхностное отношение к этим объектам. Моя позиция основана на том простом факте, что большая часть любителей в течение некоторого периода времени обязательно занимается простейшими наблюдениями двойных звезд. Цели, которые они преследуют, могут быть разными: от проверки качества оптики, спортивный интерес, до более солидных задач типа собственными глазами в течение нескольких лет пронаблюдать изменения в далеких звездных системах. Еще один момент, почему наблюдение может иметь ценность - это тренировка наблюдателя. Постоянно занимаясь двойными звездами, наблюдатель может содержать себя в хорошей форме, что может в дальнейшем помочь при наблюдениях других объектов, увеличивает способность подмечать незначительные и второстепенные детали. Примером может служить история, когда один из моих соратников, потратив несколько выходных дней, пытался разрешить пару звезд в 1" используя 110мм. рефлектор, и, в конце концов, добился результата, когда мне, в свою очередь, пришлось спасовать с более крупным 150мм. инструментом. Может все эти цели и не является первостепенными задачами у любителей, но, тем не менее, такие наблюдения проводятся, как правило, периодически, а потому эта тема нуждается в дополнительном раскрытии и некотором упорядочивании ранее собранного известного материала.
Взглянув на хороший любительский звездный атлас, вы наверняка заметите, что очень большая часть звезд на небе имеет своего спутника или даже целую группу звезд-спутников, которые, подчиняясь законам небесной механики, совершают свое занимательное движение вокруг общего центра масс на протяжении нескольких сотен лет, тысяч, а то и сотни тысяч лет. Только только получив в свое распоряжение телескоп, многие сразу наводят его на хорошо известную красивую двойную или кратную систему и иногда такое простое и незамысловатое наблюдение определяет отношение человека к астрономии в будущем, формирует картину его личного отношения к восприятию вселенной в целом. Я с умилением вспоминаю свой первый опыт таких наблюдений и думаю, что и вам найдется, что рассказать об этом, но в тот первый раз, когда в далеком детстве я получил в подарок 65 миллиметровый телескоп, один из первых моих объектов, который взял из книги Дагаева "Наблюдения звездного неба", была красивейшая двойная система Альбирео. Когда ведешь свой маленький телескоп по небу и там, в очерченном кружке поля зрения, проплывают сотни и сотни звезд Млечного Пути, а потом появляется красивая пара звезд, которые настолько контрастно выделены относительно всей оставшейся основной массы, что все те слова, что сформировались у вас для воспевания великолепия красот неба разом исчезают, оставляя вас лишь потрясенным, от сознания того, что величие и красота холодного космоса намного выше тех банальных слов, что едва вы не произнесли. Такое наверняка не забывается, даже через множество прошедших лет. Телескоп и наблюдатель Для раскрытия основ наблюдения таких звезд можно использовать буквально лишь пару общих выражений. Все это можно просто описать как угловое разделение двух звезд и измерение расстояния между ними на текущую эпоху. На поверку оказывается, что все далеко не так просто и не однозначно. При наблюдении начинают проявляться различного рода сторонние факторы, которые не позволяют вам достичь без некоторых ухищрений нужного вам результата. Возможно, что вам уже известно о существовании такого определения, как предел Дэвиса. Это давно известная величина, которая ограничивает предел возможностей некоторой оптической системы в разделении двух близко расположенных объектов. Другим языком изъясняясь, использовав другой телескоп или зрительную трубу, вы сумеете разделить (разрешить) два более тесно расположенных объекта, либо эти объекты сольются в один, и вы не будете способны разрешить эту пару звезд, то есть увидите вместо двух только одну звезду. Эта эмпирическая формула Дэвиса для рефрактора определена как: R = 120" / D (F.1) где R-минимально разрешимое угловое расстояние между двумя звездами в секундах дуги, D-диаметр телескопа в миллиметрах. Из нижеследующей таблицы (Tab.1) хорошо видно, как изменяется эта величина с увеличением входного отверстия телескопа. Однако в действительности эта величина может существенно колебаться у двух телескопов даже с одинаковым диаметром объектива. Это может зависеть от типа оптической системы, от качества изготовления оптики, ну и, разумеется, от состояния атмосферы.
Что нужно иметь для того, чтобы приступить к наблюдениям. Самое главное, конечно, телескоп. Необходимо отметить, что многие любители неправильно трактуют формулу Дэвиса, полагая, что только она определяет возможность разрешения тесной двойной пары. Это не правильно. Несколько лет назад я встречался с одним любителем, который жаловался на то, что вот уже в течение нескольких сезонов не может разделить в 2.5 дюймовый телескоп пару звезд, между которыми всего лишь 3 угловые секунды. В действительности оказалось, что он пытался сделать это, используя небольшое увеличение в 25 крат, аргументируя это тем, что с таким увеличением у него лучше видимость. Безусловно, он был прав в одном, меньшее увеличение значительно уменьшает вредное влияние воздушных потоков в атмосфере, но основная ошибка заключалась в том, что он не принял во внимание еще один параметр, влияющий на успешность разделения тесной пары. Я говорю о величине известной под названием "разрешающее увеличение". P = 0.5 * D (F.2) Формулу вычисления этой величины я не так часто встречал в других статьях и книгах, как описание предела Дэвиса, потому, наверное, и возникло у человека такое заблуждение насчет способности разрешить тесную пару при минимальном увеличении. Правда надо ясно себе отдавать отчет в том, что эта формула дает увеличение, когда уже можно наблюдать дифракционную картину у звезд, а соответственно, и близко расположенного второго компонента. Еще раз подчеркну слово наблюдать. Так как для проведения измерений значение этого увеличения необходимо умножить как минимум раза в 4, если позволяют атмосферные условия. Несколько слов о дифракционной картине. Если вы взглянете на относительно яркую звезду в телескоп при максимально возможном увеличении, тогда заметите, что звезда выглядит не как точка, как это должно быть в теории при наблюдении очень далекого объекта, а как кружочек небольшого размера, окруженный несколькими кольцами (так называемые дифракционные кольца). Понятно, что количество и яркость таких колец непосредственно влияет на легкость, с которой вы сможете разделить тесную пару. Может так получиться, что слабый компонент просто будет растворен в дифракционной картине, и вы не сумеете выделить его на фоне ярких и частых колец. Интенсивность их зависит напрямую как от качества оптики, так и от коэффициента экранирования вторичным зеркалом в случае использования рефлектора или катадиоптрической системы. Вторая величина, конечно, не вносит серьезные коррективы в возможность разрешения некоторой пары в общем, но с увеличением экранирования падает контраст слабого компонента относительно фона.
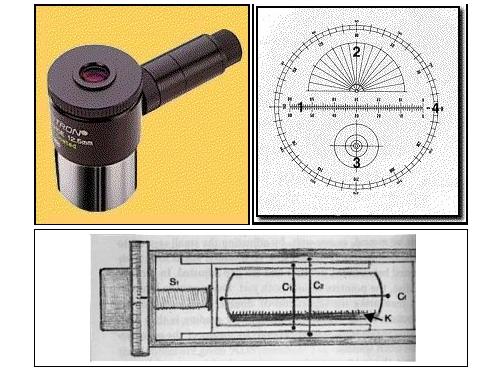
Кроме телескопа, разумеется, потребуется еще и измерительные приборы. Если вы не собираетесь вести измерения положения компонентов относительно друг друга, то можно, в общем, обойтись и без них. Скажем, вас вполне может устроить сам факт того, что вам удалось сделать разрешение близко расположенных звезд вашим инструментом и убедится, что стабильность атмосферы сегодня подходящая или ваш телескоп дает хорошие показатели, и вы еще не утратили былых навыков и сноровку. Для более глубоких и серьезных целей необходимо использовать микрометр и часовую шкалу. Иногда такие два прибора можно встретить в одном специальном окуляре, в фокусе которого устанавливается стеклянная пластинка с нанесенными тонкими линиями. Обычно риски наносятся через определенные расстояния с помощью лазера в заводских условиях. Вид одного такого, промышленно выпускаемого окуляра приведен рядом. Там не только сделаны отметки через каждые 0.01 мкм, но и по краю поля зрения размечена часовая шкала для определения позиционного угла.
Такие окуляры довольно дороги и часто приходится прибегать к другим, обычно самодельным, устройствам. Можно в течение некоторого времени спроектировать и изготовить самодельный проволочный микрометр. Суть его конструкции в том, что одна из двух очень тонких проволочек может двигаться относительно другой, если вращается кольцо с нанесенными на него делениями. Через соответствующие передачи можно добиться того, что полный поворот такого кольца дает очень незначительное изменение расстояния между проволочками. Конечно, такой прибор будет нуждаться в очень длительной калибровке, до тех пор, пока не будет найдено точное значение одного деления такого устройства. Зато оно доступно в изготовлении. Эти устройства, и окуляр, и микрометр требуют для нормальной работы некоторых дополнительных усилий со стороны наблюдателя. Оба работают по принципу измерения линейных расстояний. Как следствие возникает необходимость связать две меры (линейную и угловую) воедино. Это, возможно, сделать двумя путями, определив опытным путем из наблюдений величину одного деления обоих приспособлений, или рассчитав теоретически. Второй метод не может быть рекомендован, так как базируется на точных данных о фокусном расстоянии оптических элементов телескопа, но если это известно с достаточной точностью, то угловая и линейная меры могут быть связаны соотношением: A = 206265" / F (F.3) Это дает нам угловую величину объекта расположенного в главном фокусе телескопа (F) и размером в 1 мм.. Если это сказать проще, тогда один миллиметр в главном фокусе 2000мм телескопа будет эквивалентен 1.72 угловой минуте. Первый способ на поверку оказывается чаще более точным, но требует значительного времени. Разместите любой из типов измерительных приборов на телескоп и навидитесь на звезду с известными координатами. Остановите часовой механизм телескопа и засеките время, за которое звезда проходит путь от одного деления к другому. Полученные несколько результатов усредняются и угловое расстояние, соответствующее положению двух отметок, вычисляется по формуле: A = 15 * t * COS(D) (F.4) Проведение измерений Как уже отмечалось задачи, которые ставятся перед наблюдателем двойных звезд сводятся к двум простым вещам - разделение на компоненты и измерение. Если все описанное ранее служит помочь решению первой задачи, определить возможность выполнения таковой и содержит некоторое количество теоретического материала, то в этой части рассматриваются вопросы непосредственно относящиеся к процессу измерения звездной пары. Для решения этой задачи необходимо провести всего лишь измерение пары величин.  Позиционный угол Позиционный угол
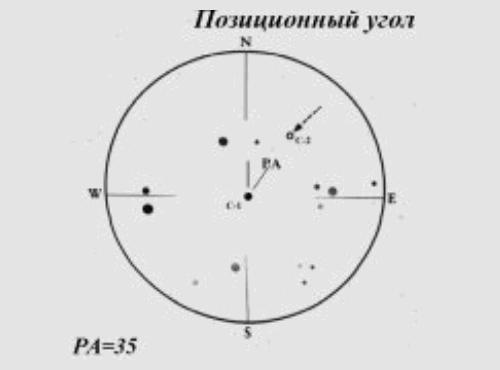
Эта величина используется для описания направления одного объекта относительно другого, или для уверенного позиционирования на небесной сфере. В нашем случае это включает в себя определение положения второго (более слабого) компонента относительно более яркого. В астрономии позиционный угол измеряется от точки направления на север (0°) и далее в сторону востока (90°), юга (180°) и запада (270°). Две звезды с одинаковым прямым восхождением имеют позиционный угол 0° или 180°. В случае, если они имеют одинаковое склонение, угол будет равен либо 90°, либо 270°. Точное значение будет зависеть от расположения этих звезд относительно друг друга (какая правее, какая выше и так далее) и того, какая из этих звезд будет выбрана как точка отсчета. В случае двойных звезд за такую точку всегда принимается более яркий компонент. До того как будет проводится измерение позиционного угла необходимо правильно сориентировать измерительную шкалу согласно сторонам света. Рассмотрим как это должно происходить при использовании окуляра-микрометра. Поместив звезду в центр поля зрения и выключив часовой механизм мы заставляем звезду перемещаться в поле зрения телескопа с востока на запад. Точка в которой звезда будет выходить за границы поля зрения и есть точка направления на запад. Если окуляр имеет угловую шкалу по краю поля зрения, то вращая окуляр необходимо установить в точке, где звезда покидает поле зрения значение 270 градусов. Проверить правильность установки можно сдвинув телескоп так, чтобы звезда только стала появляться из-за границы видимости. Эта точка должна совпадать с отметкой 90 градусов, а звезда в ходе своего движения должна пройти точку центра и начать выходить за пределы поля зрения ровно в отметке 270 градусов. После этой процедуры остается разобраться с ориентацией оси север-юг. Необходимо, правда, помнить, что телескоп может давать как телескопическое изображение (случай полностью перевернутого изображения по двум осям), так и перевернутого только по одной оси (в случае использования зенитной призмы или отклоняющего зеркала). Если теперь навестись на интересующую нас звездную пару, то поместив главную звезду в центр, достаточно снять показания угла второго компонента. Такие измерения конечно лучше всего проводить при максимально возможном для вас увеличении.  Измерение углов Измерение углов
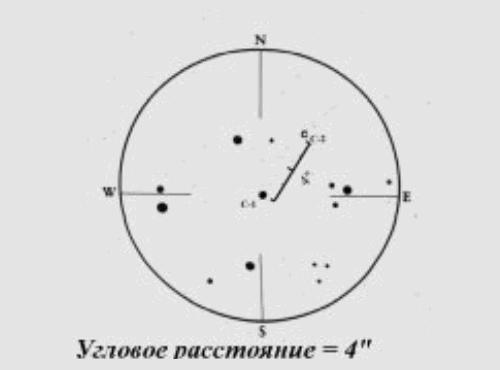
По правде говоря, самая сложная часть работы была уже проделана, как это описано в предыдущем разделе. Остается только снять результаты измерения угла между звездами со шкалы микрометра. Особых хитростей здесь нет и методы получения результата зависят от конкретного типа микрометра, но общие принятые положения я раскрою на примере самодельного проволочного микрометра. Наведите яркую звезду на первую проволочную риску в микрометре. Затем, вращая размеченное кольцо, совместите второй компонент звездной пары и вторую линию прибора. На данном этапе необходимо запомнить показания вашего микрометра для дальнейших операций. Теперь вращая микрометр на 180 градусов, и используя механизм точного движения телескопа, снова совместим первую линию в микрометре с главной звездой. Вторая отметка прибора соответственно должна оказаться в стороне от второй звезды. Подкрутив диск микрометра так, чтобы вторая отметка совпала со второй звездой и, снимая со шкалы новое значение, вычтем из него старое значение прибора для получения удвоенной величины угла. Может показаться непонятным, зачем проведена столь замысловатая процедура, когда можно было бы поступить проще сняв показания со шкалы без переворачивания микрометра. Это, безусловно легче, но в этом случае точность измерения будет несколько хуже, чем в случае использования приема двойного угла, описанного выше. Тем более что маркировка нуля на самодельном микрометре может иметь несколько сомнительную точность, а так получается, что мы не работаем с нулевым значением. Разумеется, что для получения относительно достоверных результатов нам необходимо несколько раз повторить процесс измерения угла для получения среднего результата из многочисленных наблюдений. Другая техника измерений Изложенные выше основы измерений расстояния и позиционного угла тесной пары, по сути своей являются классическими методами, применение которых можно встретить и в других отраслях астрономии, скажем селенографии. Но зачастую любителям бывает недоступен точный микрометр и приходится довольствоваться иными подручными средствами. Скажем, если у вас есть в наличии окуляр с перекрестием, то простейшие угловые измерения можно делать и с ним. Для очень тесной пары звезд он работать будет не совсем точно, но для более широких можно воспользоваться тем, что звезда со склонением d за секунду времени основываясь на формуле F.4 проходит путь в 15*Cos(d) секунд дуги. Воспользовавшись этим фактом можно засечь отрезок времени, когда оба компонента пересекают одну линию окуляра. Если позиционный угол такой звездной пары будет 90 или 270 градусов, то вам повезло, и больше никаких вычислительных действий производить не стоит, просто повторите весь процесс измерения несколько раз. Иначе, вам предстоит хитрыми подручными способами определить позиционный угол, а затем, используя тригонометрические уравнения для нахождения сторон в треугольнике, вычислить расстояние между звездами, которое должно составить величину: R = t * 15 * Cos(d) / Sin(PA) (F.5) где PA - позиционный угол второго компонента. Если произвести измерения таким образом более четырех или пяти раз, и иметь точность измерения времени (t) не хуже 0.1 секунды, то при использовании окуляра с максимально возможным увеличением, можно вполне рассчитывать на получение точности измерения до 0.5 секунды дуги или даже лучше. Разумеется, что перекрестие в окуляре должно быть расположено точно под 90 градусов и быть сориентировано согласно направлениям на различные стороны света, и что при позиционных углах близких к 0 и 180 градусам нужно слегка изменить технику измерений. В этом случае лучше слегка отклоните перекрестие градусов на 45, относительно меридиана и воспользоваться следующим методом: засекая два момента, когда оба компонента пересекают одну из линий перекрестия, получаем моменты времени t1 и t2 в секундах. За время t (t=t2-t1) звезда проходит путь в X секунд дуги: X = t * 15 * Cos(delta) (F.6) Теперь зная позиционный угол и общую ориентацию измерительной линии перекрестия в окуляре, можно дополнить предыдущее выражение вторым: X = R * | Cos(PA) + Sin(PA) | (для ориентации по линии SE-NW) (F.7) X = R * | Cos(PA) - Sin(PA) | (для ориентации по линии NE-SW) Можно сильно удаленный компонент поместить в поле зрения таким образом, что он не будет входить в поле зрения окуляра, находясь на самом его крае. В этом случае так же зная позиционный угол, время прохождения другой звезды через поле зрения и саму эту величину, можно приступить к расчетам, основываясь на вычислении длинны хорды в окружности с определенным радиусом. Позиционный угол можно попытаться определить, воспользовавшись другими звездами в поле зрения, координаты которых заранее известны. Произведя измерения расстояний между ними микрометром или секундомером, используя описанную выше технику, можно попытаться отыскать недостающие значения. Сами формулы я, конечно, здесь приводить не буду. Их описание может занять значительную часть этой статьи, тем более что их можно встретить в учебниках по геометрии. Правда несколько сложнее с тем фактом, что в идеале придется решать задачи со сферическими треугольниками, а это не то же самое, что и треугольники на плоскости. Но если вы используете такие хитрые способы измерений, то в случае двойных звезд, когда компоненты расположены близко друг к другу, вы можете упростить себе задачу, забыв о сферической тригонометрии вообще. Точность таких результатов (и без того неточных) от этого сильно пострадать не может. Лучше всего для измерения позиционного угла воспользоваться транспортиром, который используют в школах, и приспособить его для использования с окуляром. Это будет достаточно точно, а главное очень доступно. Из несложных методов измерения можно упомянуть еще один, довольно оригинальный, основанной на использовании дифракционной природы. Если одеть на входное отверстие вашего телескопа специально изготовленную решетку (чередующиеся параллельные полоски открытой апертуры и экранированной), то, разглядывая полученное изображение в телескоп, вы обнаружите серию более слабых "спутников" у видимых звезд. Угловое расстояние между "главной" звездой и "ближайшим" из двойников будет равно: P = 206265 * lambda / N (F.8) Здесь P - угловое расстояние между двойником и основным изображением, N - сумма ширины открытого и экранированного участков описанного приспособления, а lambda - длинна волны света (560nm - максимальная чувствительность глаза). Если теперь замерить три угла, воспользовавшись доступным вам типом прибора для измерения позиционных углов, то можно опереться на формулу и вычислить угловое расстояние между компонентами, опираясь на описанный выше феномен и позиционные углы: R = P * Sin | PA1 - PA | / Sin | PA2 - PA | (F.10) Величина P была описана выше, а углы PA, PA1 и PA2 определяются как: PA - позиционный угол второго компонента системы относительно главного изображения главной звезды; PA1 - позиционный угол главного изображения главной звезды, относительно вторичного изображения главной звезды плюс 180 градусов; PA2 - позиционный угол главного изображения второго компонента, относительно вторичного изображения главной звезды. Как главный недостаток следует отметить, что при использовании этого метода наблюдаются большие потери в яркости звезд (более 1.5-2.0m) и хорошо работает только на ярких парах с маленьким различием в блеске. С другой стороны, современные методы в астрономии позволили сделать рывок и в наблюдении двойных. Фотографирование и CCD астрономия позволяют нам по-новому взглянуть на процесс получения результатов. И в случае CCD изображения, и с фотографическим снимком имеет место метод измерения количества пикселей, либо линейного расстояния между парой звезд. После калибровки изображения, посредством вычисления величины одной единицы, основываясь на других звездах, чьи координаты заранее известны, вы вычисляете искомые значения. Использование CCD намного предпочтительней. В этом случае точность измерения может быть на порядок выше, чем при визуальном или фотографическом методе. CCD высокого разрешения может регистрировать очень близкие пары, а последующая обработка различными программами для астрометрии может не только облегчить весь процесс, но и дать крайне высокую точность до нескольких десятых, а то и сотых, долей угловой секунды. ЧАСТЬ I - ЧАСТЬ II
Источник:
| |||||||||||||||||||||||||||||||||||||||||
|
|